While dealing with various problems, we might come up with different types of solutions for the same problem. Although, the objective of all the solutions might be same, they may require different amount of time while serving their purpose.

Here we’ll be going through two such techniques of problem solving, applicable on various problems, which will intend to provide the same answer but may differ in the time taken to reach the solution.

Recursion

Recursive function: A function calling itself by passing required set of parameters while executing the code is called as a recursive function. The process of a function calling itself for further execution of the code is called as Recursion.

In most of the cases where the problem can be divided in optimal subproblems (i.e. optimal substructure problem), we can use recursion to find the solution.

While solving various problems with optimal-substructure using recursion, we might find the recursive function computing the solution for same sub-problem more than once which is considered to be inefficient in most of the cases.

Let’s understand it by finding the Nth element of the Fibonacci sequence:

Fibonacci Sequence: It is a sequence where the first two elements are 0 and 1 and the subsequent numbers are the sum of previous two numbers.

Example :  0, 1, 1, 2, 3, 5, 8, 13,…

As we know that barring first two positions, values at all other positions are the sum of the values at previous two locations

i.e. fib(n)=fib(n-1)+fib(n-2)

now, similarly

fib(n-1)=fib(n-2)+fib(n-3)

fib(n-2)=fib(n-3)+fib(n-4)

and so on.

Now we will be creating a function to recursively carry out the above process

Following is the code snippet of that function

Time Complexity: O(2^n)

Let’s check what is exactly happening here through the following structure of recursion in n=5 case.

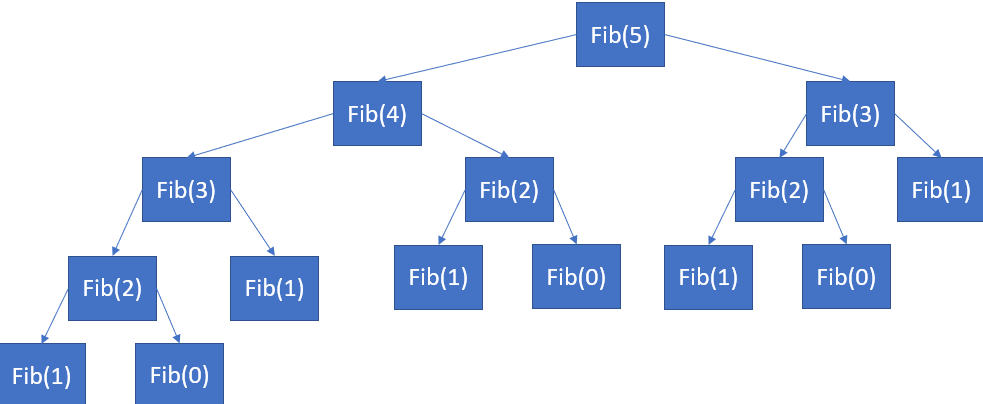
Before moving to our next section, we should have a short glimpse over the above recursion structure. Here we can observe that we have calculated Fibonacci value of some numbers at multiple occasions which leads to increase in number of operations significantly. This is the issue that we will try to address using Dynamic programming.

Dynamic Programming

To optimize the above recursive solution we can either,

Modify the recursive solution so that it would not calculate a subproblem more than once

OR

Find an optimized approach without recursion.

The solution of above two approaches could be acheived by using Memoization and Tabulation techniques of dynamic programming.

Memoization (Top-Down approach)

It optimizes the recursive solution by storing the solution of every subproblem in a sequence so that when the need arises to find the same solution again, it can be done by taking it from that sequence rather than calculating it again.

Here is the code snippet after optimizing the initial recursive approach.

Time Complexity: O(n)

The effect of this optimization can be seen through the structure of recursion.

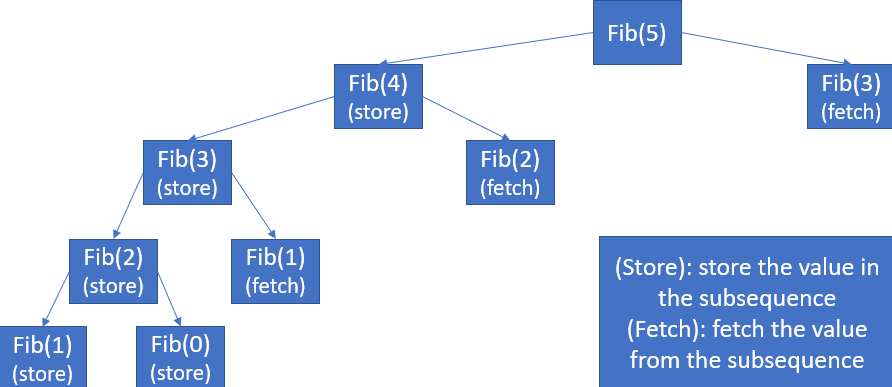
Why is Memoization called as the Top-Down approach?

As in the current example, we first intended to calculate the Fibonacci value of nth number and as per the requirement we moved on to the smaller subproblems i.e. we moved from larger subproblems to the smaller subproblems and subsequently reached the solution. Hence, Memoization is also referred as the Top-Down approach;

Tabulation (Bottom-Up approach)

In this approach we will reach the solution to the main problem by calculating solution of all its subproblems starting from the smallest subproblem without using recursion.

As in our current example of Fibonacci sequence, rather than calling function recursively and getting solution of every subproblem, we can just keep on calculating sum of previous two numbers up-to n.

Here is the code snippet of the tabulation approach of our example:

Time Complexity: O(n)

Why is tabulation called as the Bottom-up approach?

Considering the current example, in tabulation approach, we started computing values of subproblems from 0^th position to the n^th   position in other words from smallest subproblem to the largest subproblem. Hence, tabulation is termed as Bottom-up approach.

While comparing general recursive solution with Dynamic programming solutions, we can clearly see that optimization of recursive solution using DP significantly affects the performance of our code.

For applying Both of the above approach you should consider solving:

1. Longest increasing Subsequence problem
2. Longest common subsequence problem