Relation between DP and DAG
DAG (Directed Acyclic Graph) :
· It is a directed graph with no directed closed path.
· It consists of vertices and edges, and we cannot reach the same vertex when we start from that vertex and follow a continuous path.
· Nodes of a DAG can be linearized; that is, we can have a sequence from left to right connecting vertices.
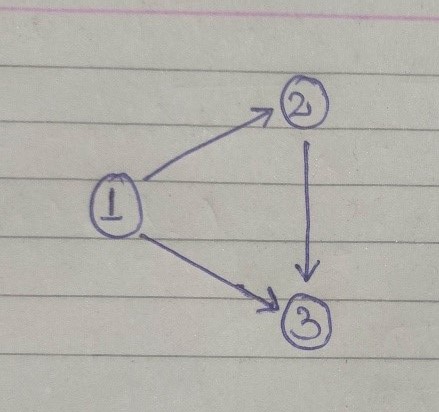
· Above figure is an example of DAG. Clearly, we can see that nodes are linearized. For example, if I start from node 1 then there are 2 paths from 1 to reach 3. 1 -> 2 -> 3 and 1 -> 3 are the two paths.
· We can observe that there is some kind of topological ordering of the nodes ,i.e, some kind of ordering from top to bottom.
· This observation is used in DP.
Relation between DP and DAG :
· Dynamic programming is all about finding subproblems and relating those subproblems (or merging them) to obtain the solution to larger problem.
· In DP programming we are not given a DAG to solve. It’s hidden.
· Its nodes are subproblems and edges are a type of recursive condition by which we connect the vertices. Its root node is the base condition.
· In DP, we start from the main problem and then divide it into smaller problems and go to the smaller subproblems using some recursive condition.
· Similarly, we can relate it with DAG. We traverse nodes (which are subproblems) and for traversal we have to go through edges (which is a type of recursive condition which we write in DP).
· If solving problem B requires the answer of subproblem A, then there is a (conceptual) edge from A to B. By this way, connecting all the vertices we will get a DAG.
Example :
Longest Increasing Subsequence
The Longest Increasing Subsequence (LIS) problem is to find a longest subsequence in which elements are sorted in ascending order.
For example, the length of LIS for {5,6,2,8} is 3 and LIS is {5,6,8}.
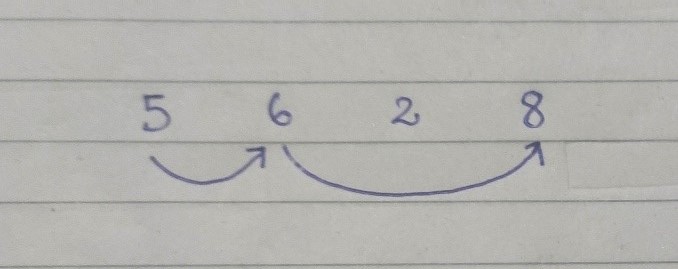
DAG idea :
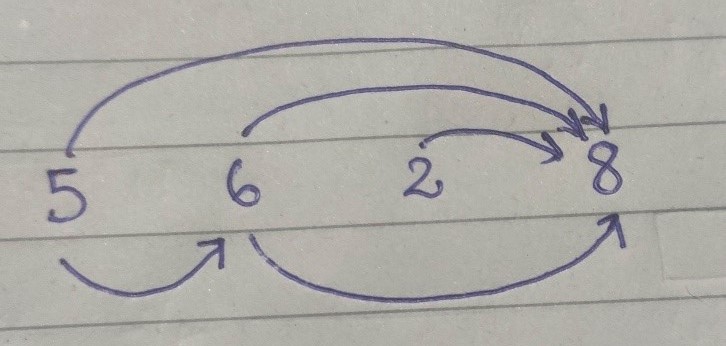
· In this example, the arrows denotes all the possible paths from a node to another node, i.e., there is a directed edge from lower number to each higher number.
· As a whole, it is a DAG.
· To find the longest increasing subsequence, we have to find the longest path in the DAG created above.
· So, our problem is reduced to find the longest path in DAG.
· To find that, its straightforward that from each node we have to find that node which is connected to it and has the longest path among those connected nodes.
· Infact we can see that most of the DP problems can be finally resolved into some kind of DAG, in which edges will represent the recursive condition/traversal condition and nodes are the sub-problems.
Practice Problem :
Happy Coding 😊
By Programmers Army
Contributed by Shubham Kumar