Sorting Algorithms - Merge Sort
Merge sort also uses divide and conquer technique for sorting, but unlike quick sort, it requires some additional memory. It is one of the most efficient sorting algorithms.
Merge sort divides the sequence in two halves and then treats those two halves as a sequence and keeps on dividing these sub-sequences in two halves until we can’t divide them anymore.
Now we will start merging those divided parts in the same order in which they were separated but, while merging two sub sequences, we will pick the smallest element available in both sub sequences and place it in the new subsequence.
This will be done until both sub-sequences are empty which will ensure that the new subsequence generated after merging these two sub sequences has all the elements in placed ascending order.
This process of merging sub-sequences will be continued until the sub-sequence has a length equal to the original sequence.
Unlike quick sort, merge sort requires O(N) extra space while storing the small sub-sequences.
Worst case time complexity of merge sort is O(n*log(n))
The visualisation of merge sort is as follows:
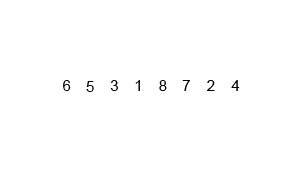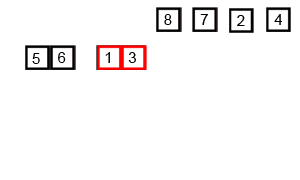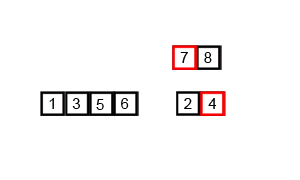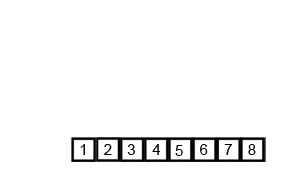
Implementation of merge sort is as follows:
Time Complexity : O( n logn )
So that’s it for this article we will be coming up with our next article on further topics very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding 😊
By Programmers Army