Convex Hull Part 2 – Graham Scan
If you haven’t seen part 1, have a look on it to understand this algorithm better, here again we are going to find the boundary of some given set of points on a 2D plane, as it had a complexity of O(n^2) by using Jarvis algorithm.
Graham scan will do this in O(n*logn), this is helpful when giving programming contests.
The idea is simple, I’ll first give a rough idea of it and then clear things in the code itself.
1. At first, we need a point to start from somewhere, either it can be the leftmost, rightmost or even bottommost. I take the bottommost point to start.
2. Now, all other points need to be sorted in some order to process, this order is needed because we can’t just process other points randomly to make our algorithm efficient.
Now that order is polar sorting, in this we sort points based on their angles, now we start iterating by taking 3 points at a time, 2 points will be our current line and third point is the point of consideration, if this third point makes a left turn then we add it( I am assuming here that we started moving from the bottommost point to its right) or else if its on right then we need to go back and remove the points that we have taken so far until we make our current point a left turning point.
I am also assuming that we have removed collinear points, because now its easy to realise why its required over here to remove some collinear points (collinear here means on a same line producing from the bottommost point). We keep on iterating over all the elements like this until we come back to our initial point. That’s it, this completes the algorithm.
Now we will dry run it over a test case and then implement the functions.
Suppose we have some points.
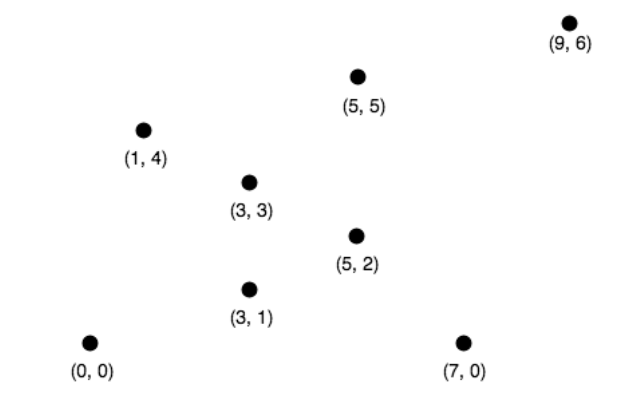
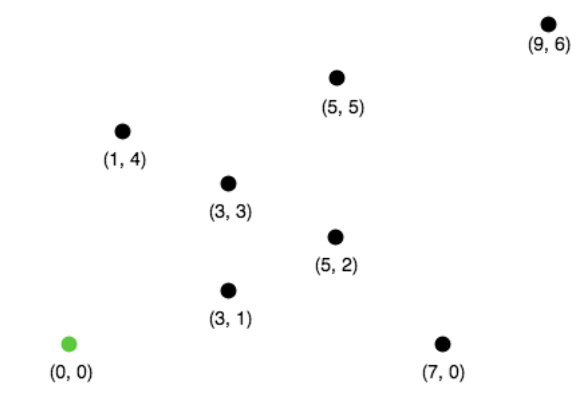
Now we will find the bottommost and leftmost point if there is a tie.
 Now, we sort points in polar order.
Now, we sort points in polar order.
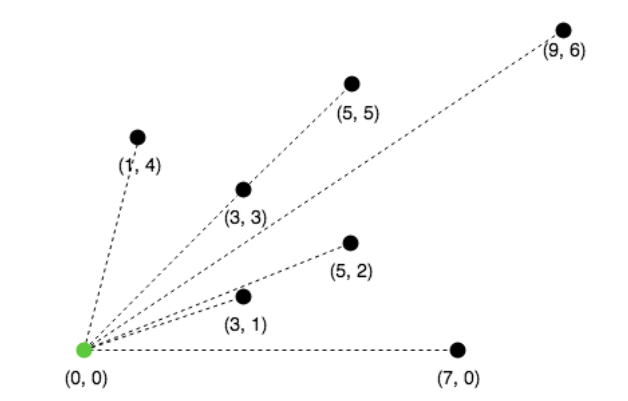
Sorted points will be
[(0,0),(7,0),(3,1),(5,2),(9,6),(3,3),(5,5),(1,4)]
Now, collinear points will be checked and the farthest from (0,0) will be kept.
Here 3,3 and 5,5 are collinear so 3,3 is discarded(shown in red)
Now, push 3 points into the stack, the first two will always in our skull because of obvious reasons.
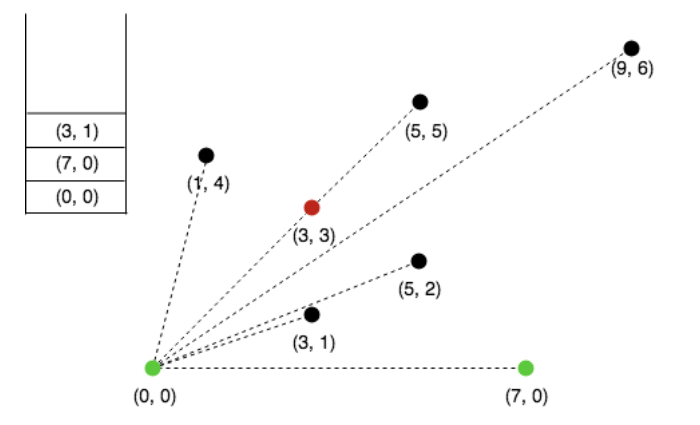
Next, consider 5,2, since its making a right turn discard the top element
from stack.
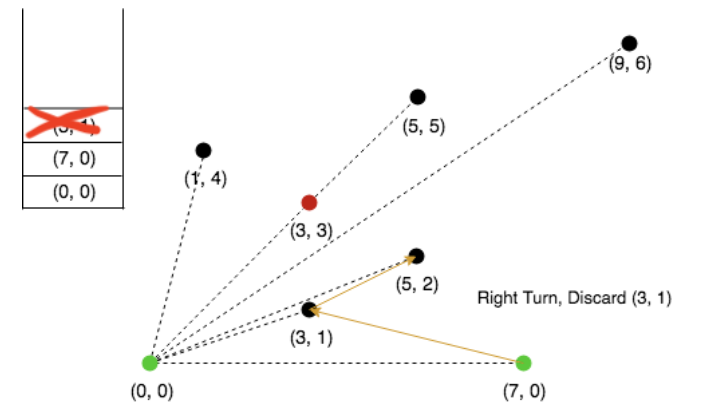
Now, 5,2 is making a left turn, push into the stack.
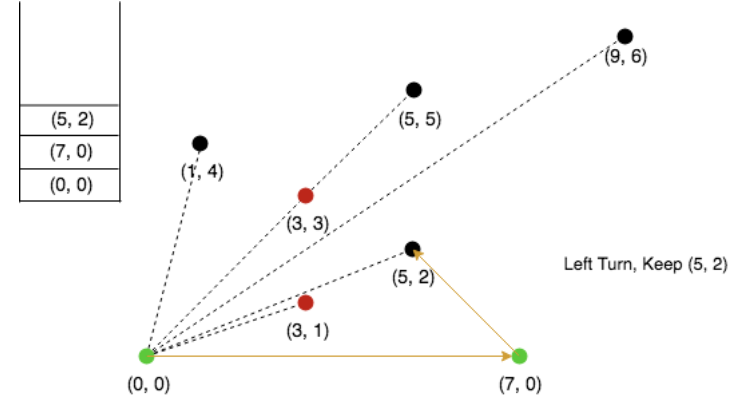
Next, 9,2 is making a right turn, discard the top element from stack.
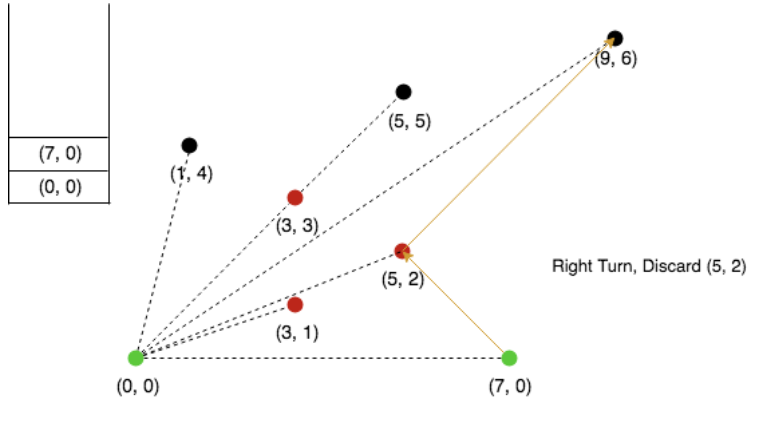
Push 9,6 in stack
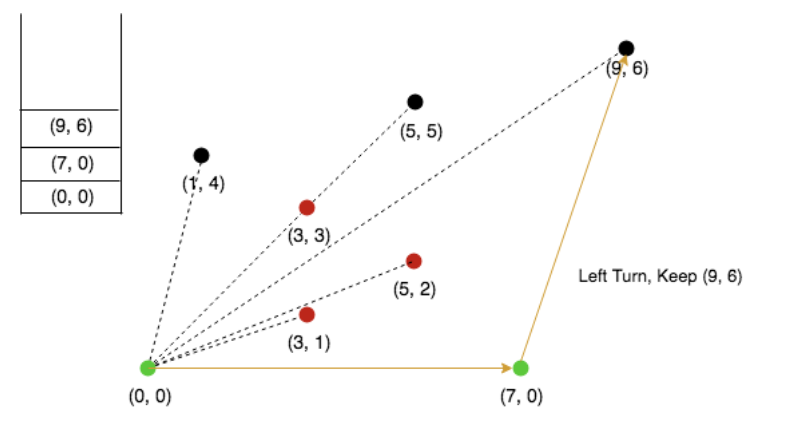
Next, 5,5 is making a left turn, push it in stack.
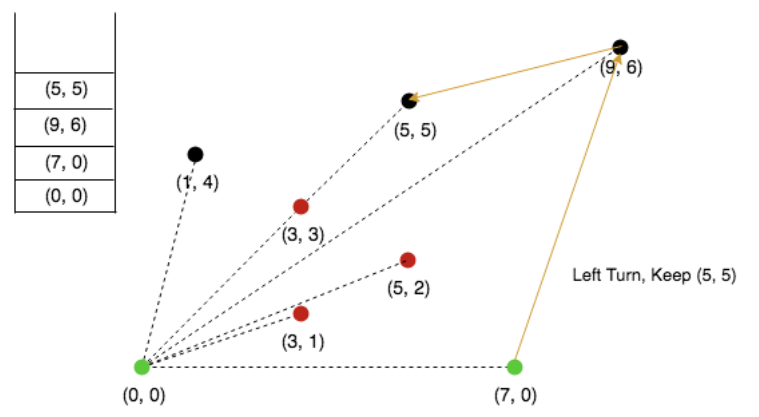
Next, 1,4 is collinear, so we will remove top element from stack.
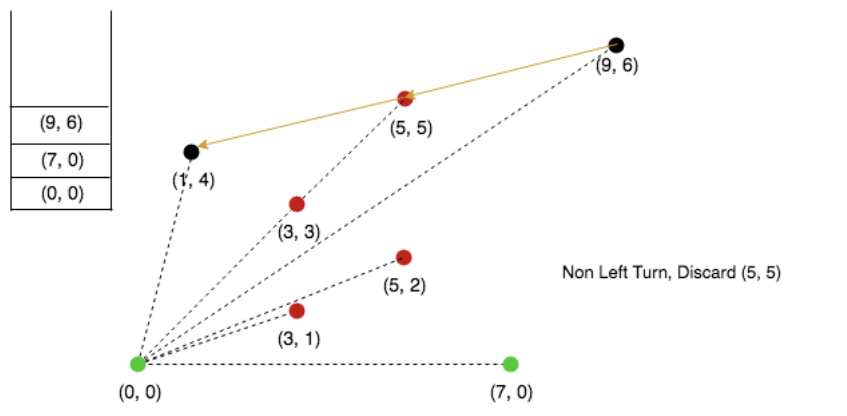
Push 1,4 in stack.
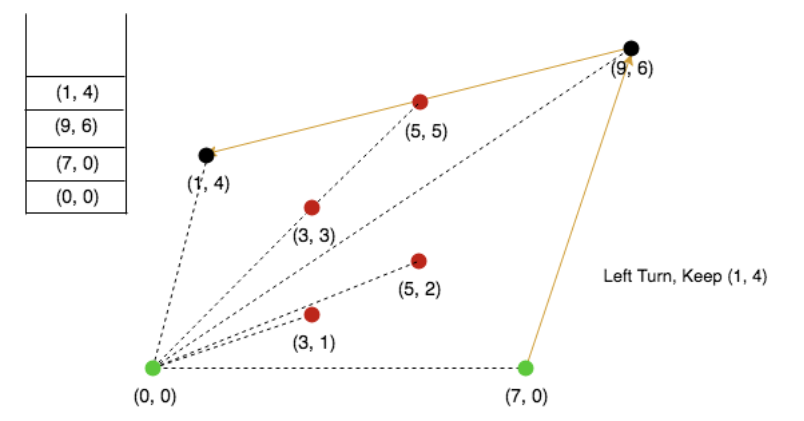
The list ends here, and the stack contains our convex hull points.
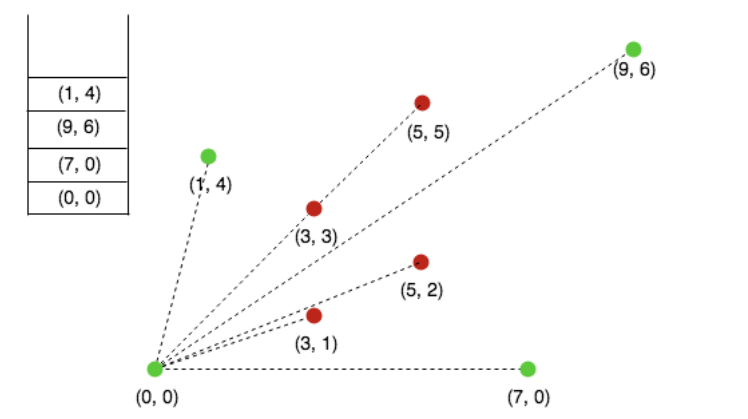
After sorting, it will take linear time to finish the algorithm.
Implementation:
Time Complexity: Overall complexity is O(n) + O(nLogn) + O(n) + O(n) which is O(nLogn)
Apart from this, there is one more implementation of graham scan, I found this one to be more intuitive and easier to implement.
After going through the code, try to write it on your own to get a better grip, that will help you to understand it clearly.
Here are some problems,
https://www.hackerearth.com/problem/algorithm/maximum-polygon-9475e95a/
References
https://algorithmtutor.com/Computational-Geometry/Convex-Hull-Algorithms-Graham-Scan/
This article is contributed by Sanchit Kumawat
So that’s it for this article we will be coming up with our next article on further topics of Algorithms very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊