Convex Hull Part 1 – Jarvis algorithms
In this article, we are going to see how we can find the boundary of any set of points.
For example, see the diagram below.
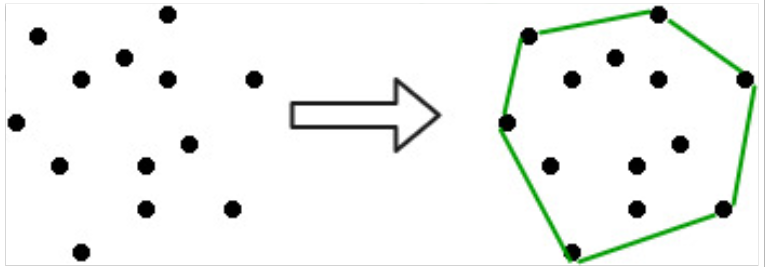
In other words, we can think of this as some rigid sticks are put on a surface and then if we stretch a rubber bank around it and leave the rubber band, then the shape it forms will be our convex hull.
In this tutorial, we are going to implement a simple approach, it’s called Jarvis algorithm.
Assume the plane is X-Y plane.
1. Suppose we have the leftmost point, ‘p’ (by X coordinate), this point would always be in our Convex hull because if it’s not then it would never be in the hull.
2. Now, we can either find the most clockwise or most anticlockwise point (q) to that leftmost point.
3. Point q belongs to the hull because, again, if it wouldn’t be on the hull then there would not be any other point who is going to cover this point.
4. So, likewise, we will keep on searching for that by keeping a track of current most, let’s say, counter clockwise point until we come back to our initial point.
5. Now let’s quickly jump to our code because there’s nothing left behind in the algorithm. Further things I have cleared in the comments of code.
Time complexity: O(n^2) as in the worst ca4se, all the points can lie on the hull itself.
Practice problems:
https://practice.geeksforgeeks.org/problems/convex-hull/0
https://brilliant.org/practice/convex-hull/
This article is contributed by Sanchit Kumawat
So that’s it for this article we will be coming up with our next article on further topics of Algorithms very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊