Inplace rotate square matrix by 90 degrees
So here we have to rotate a square matrix anti - clockwise by 90 degree.
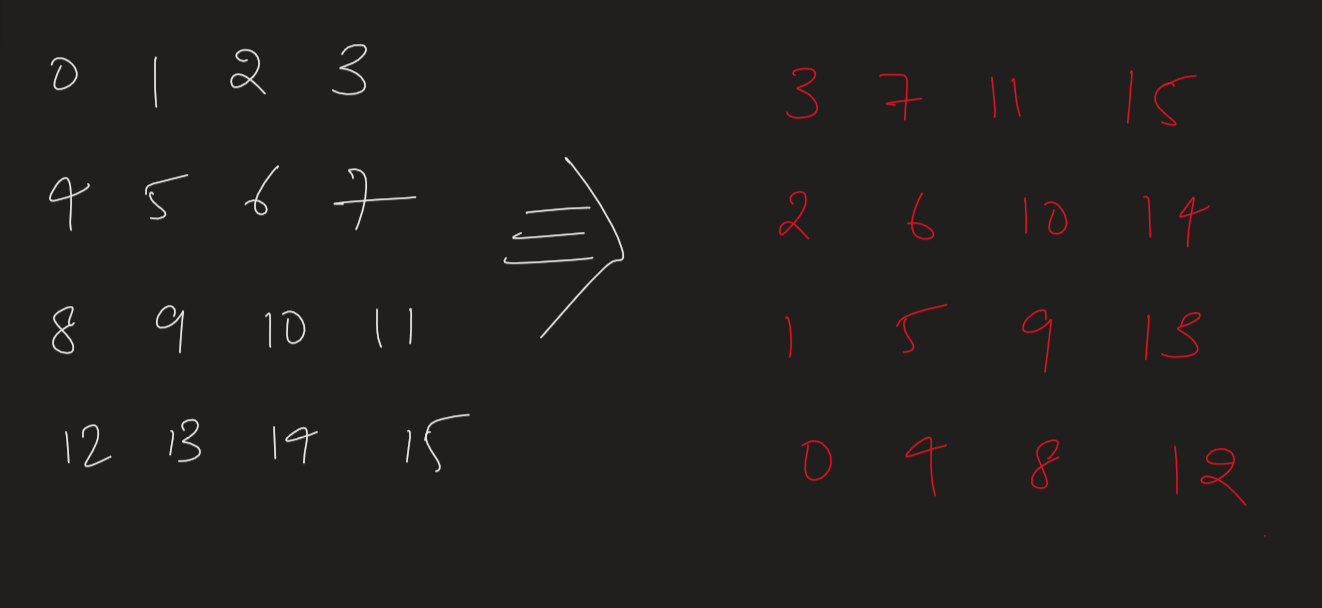
BASIC IDEA -
So its a very simple observation that the columns are converted to rows now. The last column will be out first row, second last column becomes 2nd row and so on.
Code -
Output -
Time and space analysis -
Time complexity is O(n2) and space complexity is also O(n2)
BUT CAN WE DO BETTER ???????
Yes we can decrease the space complexity.
IDEA -
Instead of making columns to rows. Let's rotate the outer square first.
And then the inner square and so on. And rotating squares can be done in O(1) space complexity.
The Squares to be rotated looks like this.

So there will be floor of (n/2) squares in a n square matrix.
We can map the following positions in a pair of 4 and do the clockwise rotation by hand of there pairs.

We can observe the if we’re at the i th square .
Then the pairs will be
(i,j),(j,n-i-1),(n-i-1,n-j-1),(n-j-1,i) where i will be from (0,n//2) and j will be from (i,n-i-1).
CODE -
Output -

Time and space analysis -
Time complexity is again O(n2) but the space complexity here is O(1)
Practice Problems -
1. https://www.interviewbit.com/problems/rotate-matrix/
2. https://www.hackerrank.com/challenges/matrix-rotation-algo/problem
3. https://leetcode.com/problems/rotate-image/
This article is contributed by Satwik Tiwari
So that’s it for this article we will be coming up with our next article on further topics of Algorithms very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊