Sort nearly sorted (K- Sorted) Array


Problem Statement -

The K sorted array is a problem where we have an array which is almost sorted and the given k represents that an element is atmost k units shifted to its right or left than its actual position in sorted array

I.e the element in the sorted array at position ith must be in [i-k,i+k] indexes in given array .


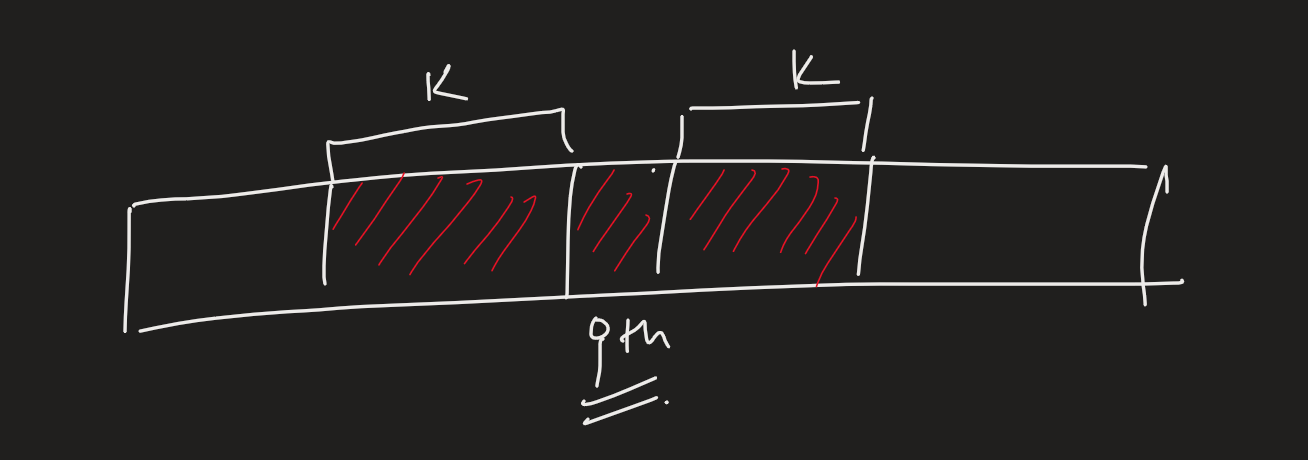
So we can normally sort the array in worst time complexity of O(nlogn) . which doesn’t even take this k in account. (k == n) case.

But can we do better?? . . . .

Yes, We can use the idea that the let the array is sorted till index i.

So the i+1 th element of the sorted array must be someone from the next K+1 elements. And which will be the smallest element from the next k+1 elements.

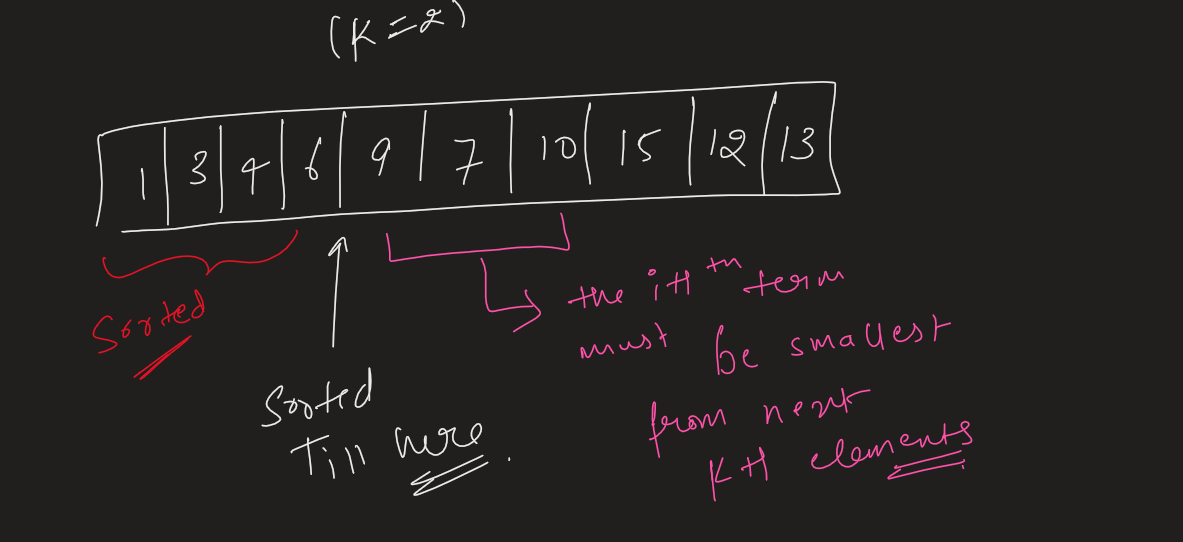
So this gives us hint to use Min heap here.

Approach -

Lets make a min heap of size K+1. insert all the k+1 starting elements in it . Now we know the smallest one is the 1st element in the sorted list. Pop the smallest element and append it in ans array. Now insert the next element in the heap and again pop the element which will be your 2nd element in sorted list and so on.

CODE -

TIME ANALYSIS -

For the given code. We are using heappop and heappush for n times almost which gives us the overall complexity of O(n logk). As there are atmax K elements in the Min heap at any moment providing the push and pop operation in logk time.


It is highly recommended to solve below problems, they are handpicked by Programmers Army:

Practice Problems :-

• https://www.hackerrank.com/challenges/almost-sorted/problem

• https://www.spoj.com/problems/BTCODE_K/

• https://www.hackerearth.com/practice/algorithms/sorting/merge-sort/practice-problems/algorithm/the-sorted-array/


This article is contributed by Satwik Tiwari

So that’s it for this article we will be coming up with our next article on further topics of Algorithms very soon till then keep learning, keep coding, keep reading and keep improving !!

Happy Coding

By Programmers Army 😊