Number of ways to reach destination in a Maze
We have to find the number of ways in which we can travel from (1,1) to (R,C) in a grid of RxC by just moving Right and Down and not walking through the obstacles.
For example ,
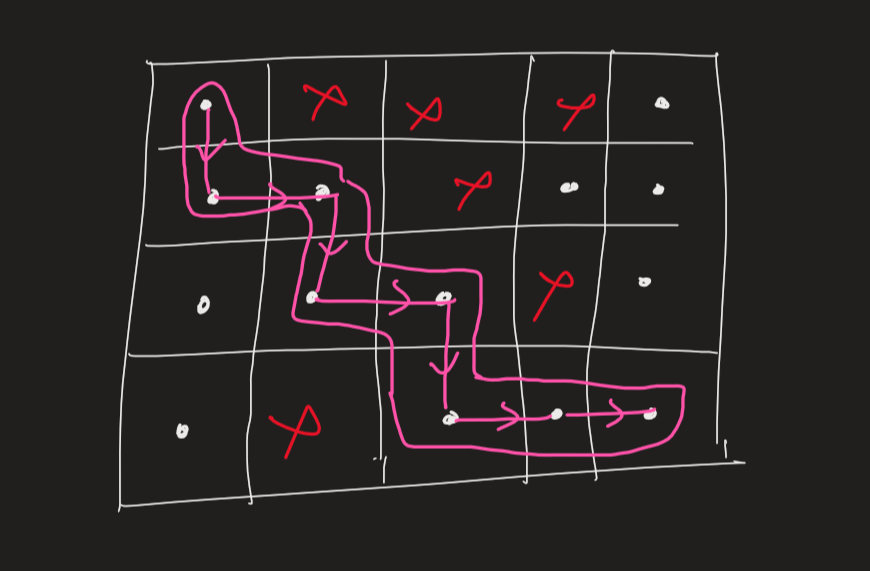
The shown path is the only path from (1,1) to the (4,5) . hence the answer to this example is 1.
So how to solve for large random grids.
Naive recursive approach Idea -
Given a grid. Starting from (1,1) . if we can go to the right block then
Lets call a recursion to the right block and similarly if we can go down
call recursion at down block. If we can read (R,C) then this path is valid and hence we’ll increment out counter.
So lets assume we have a grid input consists on only 1 and
Code -
Output = 9
Time Complexity -
We can see the time complexity of this algorithm is very bad, its just a naive recursion and hence
The time complexity is O(2**(n2)) .
Can we do better? Obviously .
Idea -
We can use a sort of dynamic programming idea .
dp[i][j] be the number of Ways to reach at (i,j) from the starting
position.
So we can see that:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
As we can only come to (i,j) from (i-1,j) or (i,j-1).
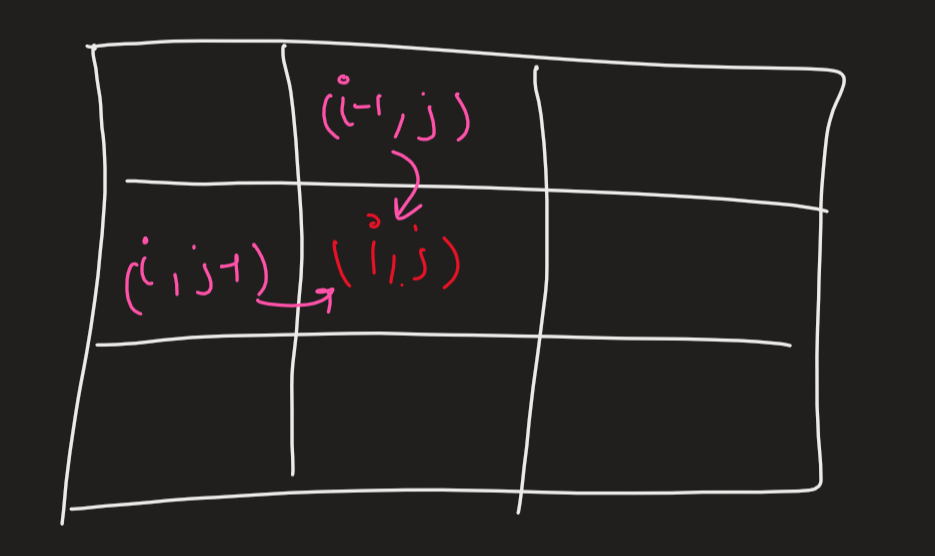
So using this recurrence we can easily solve this maze problem. And answer to our problem is dp[R-1][C-1]
Code -
Output - 9
Time Analysis -
The time complexity is clearly O(RxC) . as we’re just iterating over the grid once
This article is contributed by Satwik Tiwari
So that’s it for this article we will be coming up with our next article on further topics of Algorithms very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊