Finding connected components in an undirected graph
We have been given an undirected graph with n nodes and m edges. We are required to find all the connected components in it.
Connected components :-
• A connected component consist a group of nodes in which each node can be reached from any other node of the respective connected component. In simple words a connected component consists of set of nodes in a undirected graph that are linked to each other by paths.
• No path exists between two different connected components.
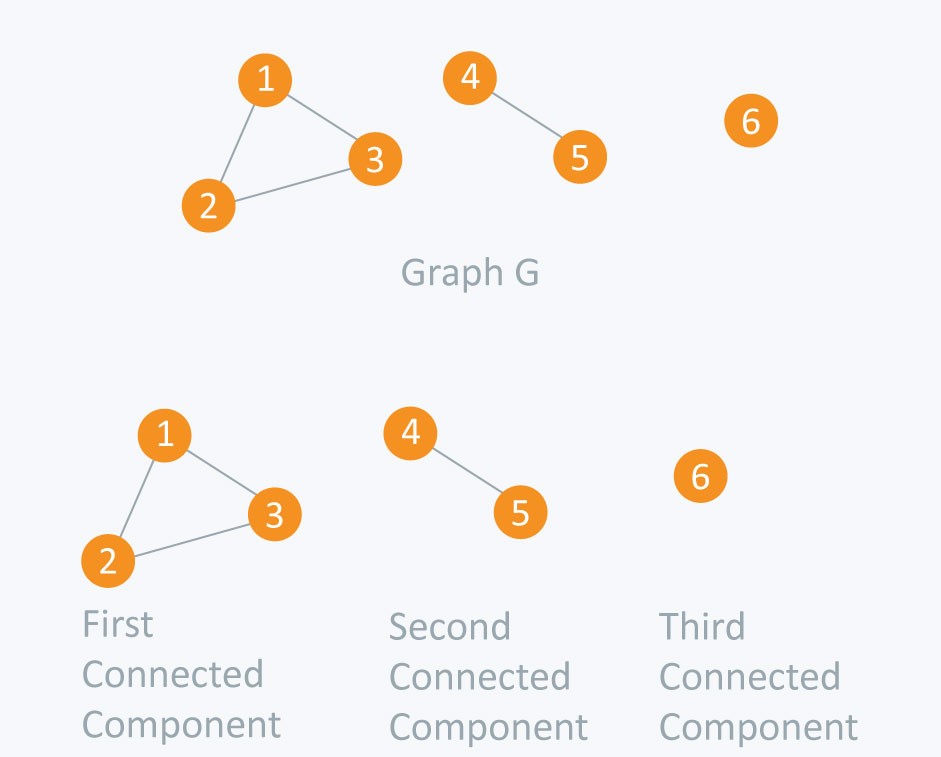
• In the above shown graph there are three connected components :-
1. First connected component consists of node 1 -> 2 -> 3 as they are linked to each other.
2. Second connected component consists of node 4 -> 5 as they are linked to each other.
3. Third connected component consist a single node 6 as no other node is linked to it.
Algorithm used:-
We can solve this problem with different methods :-
• Using Depth First Search (DFS)
• Using Breadth First Search (BFS)
1. Finding connected components using DFS :-
• We will be doing a series of DFS to solve this problem.
• Firsty we will iterate over all the nodes and check whether the node is visited or not (Initially all the nodes are unvisited).
• If a node is unvisited then we will perform DFS over that particular node which will result in traversing of all the nodes which are connected to it and marking them as visted. After which we will check for the next unvisited node and perform the DFS on it, and the same process goes on.
• Time complexity of this algorithm : O(N+M)
where N -> No of nodes in the graph
M -> No of edges in the graph
Implementation :-
Input :-
6 4
1 2
2 3
3 1
4 5
Output :-
1 2 3
4 5
6
Total number of components : 3
2. Finding connected components using BFS :-
• This algorithm is similar to the previous one with a small difference that here we use BFS for traversing the graph instead of DFS.
• Time complexity of this algorithm : O(N+M)
where N -> No of nodes in the graph
M -> No of edges in the graph
Implementation :-
Input :-
6 4
1 2
2 3
3 1
4 5
Output :-
1 2 3
4 5
6
Total number of components : 3
It is highly recommended to solve below problems, they are handpicked by Programmers Army:
Practice Problems :-
This article is contributed by Shaan Kumar
So that’s it for this article we will be coming up with our next article on further topics of Graph Theory very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊