Kth ancestor of a node in a tree


Let us see what the kth ancestor of a node means. ( assuming the kth ancestor to exist)

We know that for a node, the immediate parent of this node is 1 st ancestor of the node.

For eg.


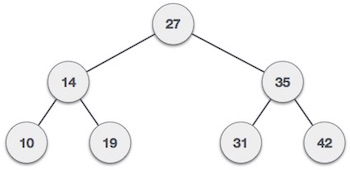
Here the immediate parent of node 19 is node 14 (also the 1st ancestor of node 19 while 27 will be the 2nd ancestor of node 19)

So the question is given a tree, we are needed to find the k-th ancestor of a certain node.





Problem statement :-

Given a tree, and a node of the tree, we need to find the k-th ancestor of the node.

Input:-

First line contains n the number of nodes in the tree and k, the index of the ancestor we are required to find out.

Then the following n-1 lines contains two space seperated integers a and b denoting the nodes connected to each other by an edge.

Last line contains node r whose k-th ancestor we need to output.

Output:-

Print the node who is kth ancestor of node r.

Constraints:-

Solution 1- O(n) Approach by using simple dfs traversal.

This was a basic O(n) solution which involved normal DFS(Depth First Search) traversal to calculate the parent and then just move one by one towards the k-th ancestor.

Why this solution is not good to go ?

This solution is good to go until there’s a slight change in the question. If there are q queries everytime asking the k-th ancestor of a certain node, out complexity with this algorithm will run directly into O(n*q) which is really poor, as if even 1<=q<=10^5, our solution will run into Time Limit Exceeded. To Improve our complexity we will be using the concept of Binary Lifting and turn our complexity into O(q*log n + n*log n) which is good to go and a huge improvement over O(n*q).

Problem statement :-

Given a tree, and a node of the tree, we need to find the k-th ancestor of the node we ask in q queries.

Input:-

First line contains n the number of nodes in the tree and k, the index of the ancestor we are required to find out.

Then the following n-1 lines contains two space seperated integers a and b denoting the nodes connected to each other by an edge.

The next line contains q the number of queries.

Then q following lines contains node r whose k-th ancestor we need to output at everyline.

Output:-

Print q lines , the kth ancestor of every node asked in the query node r.

Constraints:-

Code in C++ - Time complexity : O(n*logn+q*logn)

So our program now runs in O(n*logn+q*logn) worst case time complexity which is a huge improvement over O(n*q).

This is how we can use the method of binary lifting from a node to move up according to the given k.

The question can also be given for variable k for each query. Which is not much different from the solution I wrote. (With just a few changes ;) obviously!!!) [Might be you can try that as an exercise.]

It is highly recommended to solve below problems, they are handpicked by Programmers Army:

1. https://www.hackerearth.com/problem/algorithm/whos-your-daddy/
2. https://leetcode.com/problems/kth-ancestor-of-a-tree-node/
3. https://www.hackerrank.com/challenges/kth-ancestor/problem

This article is contributed by MD Zuhair

So that’s it for this article we will be coming up with our next article on further topics of Graph Theory very soon till then keep learning, keep coding, keep reading and keep improving !!

Happy Coding

By Programmers Army 😊