Formation of Graphs
After you guys have got an idea on the different types and classifications of graphs, we will dive into the implementation part that how we will be storing the graphs.
There are two basic types of graph storing methodology which we will be learning in this article.
These are namely,
1. Adjacency Matrix.
2. Adjacency List.
We will get to know about both of the methods mentioned above and then we will discuss which one is more convinient in a given situation.
1. Adjacency Matrix:
Adjacency matrix is the first one which we will be learning for creating and storing up of graphs. It is a really basic way of storing the graph.
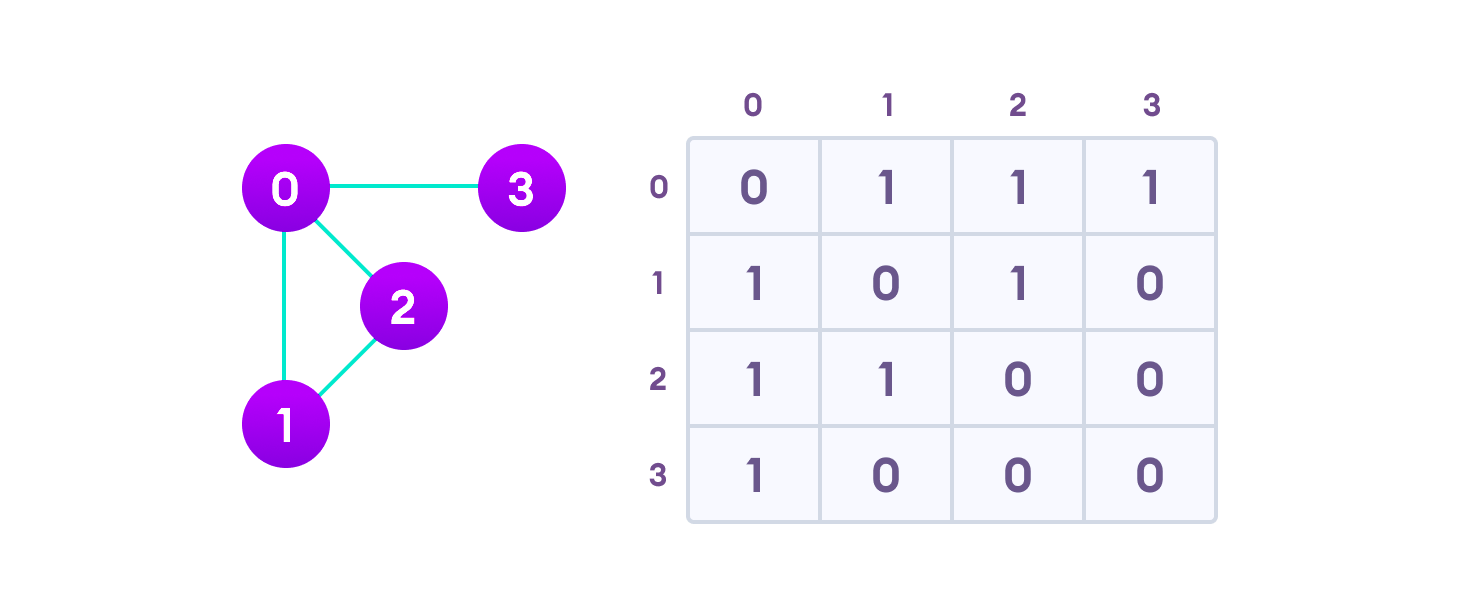
For a n vertice graph, Let A be a matrix. The adjacency matrix A is a simple n x n matrix having only 0 -1 which shows the connection between edges as the follows.
- If A[i][j]=1, it means there exists a directed edge from ith node to jth node
- else if A[i][j]=0, it means there is no edge between ith node to jth node.
So lets form a simple adjacency matrix with the given details.
Given the graph, one can easily form the matrix as follows.
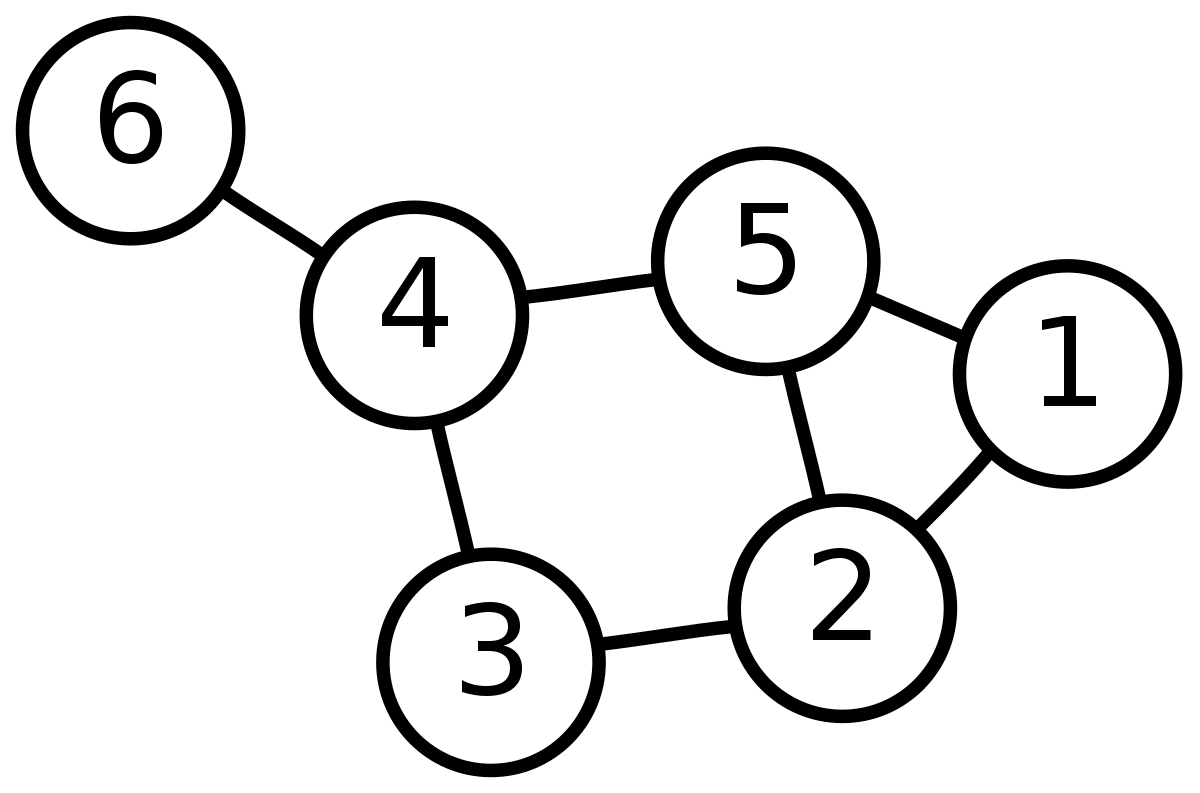
Exercise :
Write out the adjacency matrix on your own for the following graph.
Solution with code (C++):-
Note:
The above Example represents the undirected graph. Similarly, you can make it for a directed graph as well by making only one-way index nonzero that is u → v. Also, for weighted edges you just have to put weight value at index (i, j) in the adjacency matrix where i & j represents u & v respectively.
📎 Drawbacks of Adjacency matrix representation of graph :
It's Space Complexity is O(n*n), Most of the memory is useless which has 0 in its index value. Therefore if the problem has the 10^5 nodes then the size of the matrix will be (10^5 ∗ 10^5) which will exceed the maximum memory limit of a compiler. To overcome this problem Software Engineer came up with the Adjacency List.
2.Adjacency List
An adjacency list represents a graph as an array of linked lists. The indices of the array (or vector of vectors ) represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.

For the easy and efficient implementation of a adjacency list, we will be simply using a vector of vectors. (C++ STL)
For a n – node graph, we will define our adjacency list as
vector < vector <int> > v[n+1];
Lets take some example to see how it works.
Input:
First line contains the number of nodes in the graph (n) and the number of edges (k).
Then k following lines contains to space seperated integers a,b denoting the nodes connected to each other by undirected edges.
Aim : To implement adjacency list
Code in C++:
Note :
The above example represent the undirected graph in the form of adjacency list. Further if you want to implement it with the weighted graph then you can do it by using pair vector instead of integer vector which stores the (node, weight) pair with the particular node. For directed graph as well we just need to allocate node for one particular direction only u → v.
We will see now where it is convinient to use Adjacency List and Adjacency Matrix.
Let us say, we need to find if two nodes are adjacent or not.
If we use Adjacency Matrix, we can check it in constant time (O(1)).
Where as in adjacency list we will take linear time to do the same.
This is a case where using adjacency matrix will help much more.
Lets say we have a graph like 1---2---3 and we need to check whether there is any connection between 1 and 3 then using adjacency list will work in just O(n) time using any of the traversal methods. While using the adjacency matrix we have to go to every node in n*n time so a total of O(n^2) complexity to traverse hence in this case using an adjacency list will do our work faster.
This article is contributed by MD Zuhair & Rishabh Roshan
So that’s it for this article we will be coming up with our next article on further topics of Graph Theory very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊