Topological Sorting (Only for Directed)
Topological sorting of a directed graph in graph theory is just a simple linear ordering of the nodes of the graph in such a way such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.
Example-
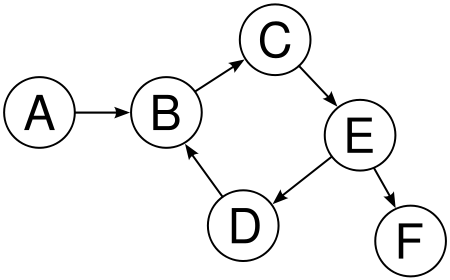
Here one of the topologically sorted sequence can be
A,B,C,E,D,F
Algorithm to find the sequence-
To find a topologically sorted sequence, the following algorithm is used.
1. We start from any vertex and apply a DFS on the node and start searching for all its childs.
2. We do DFS on a certain node until all its child are visited (using
DFS method)
3. After all the children of a the node are visited, we push that into a stack.
4. Popping out the stack after visiting all nodes through this algorithm will give us the topologically sorted sequence.
Code in C++
This article is contributed by MD Zuhair
So that’s it for this article we will be coming up with our next article on further topics of Graph Theory very soon till then keep learning, keep coding, keep reading and keep improving !!
Happy Coding
By Programmers Army 😊