It is one of the methods for searching which we generally used in Trees and Graphs data structures. Now, the question arises that,

• what type of search is this ?
• what's so unique about it ?

Somehow we can relate the idea behind this search with its name only which says we have to search depth-first 😅. Let's understand it with an example:



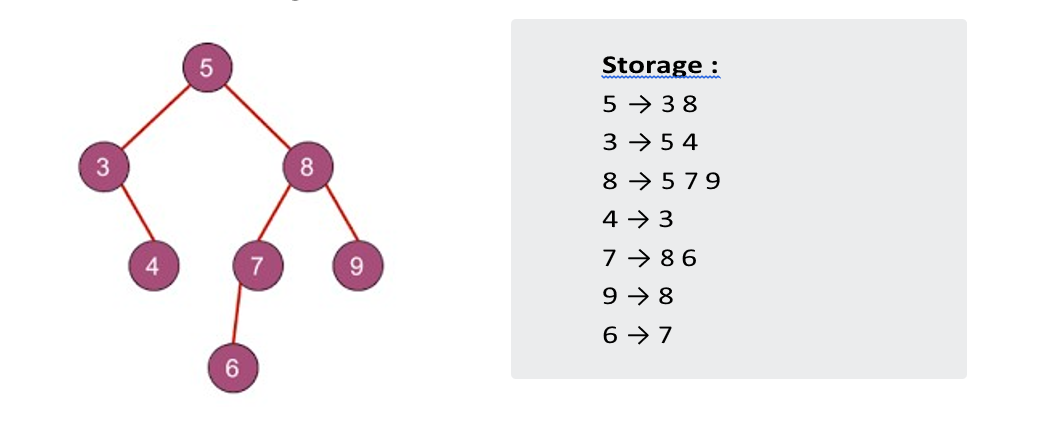
The storage part in the right-hand side determines the method of storing a tree if you are not familiar with this then read my previous article on Introduction to Trees and Graphs in which I have discussed how you can store all the values of nodes and edges in Trees as well as in Graphs.

Now, when we have to traverse the above given tree using DFS then we will start with pushing a node 5 (root node) into a stack then followed by the process given below :

• we will iterate till our stack not becomes empty and in each iteration, we pop a node element from the stack and traverse whatever adjacent nonvisited node left.

• we pop 5 and push its adjacent element → Stack : 3 8

• we pop 8 and then → Stack : 3 7 9 NOTE - we haven't push 5 (adjacent to node 8 as it's already visited.

• we pop 9, Stack : _{3 7} then pop 7 → Stack :3 6 then pop 6 .

• pop 3 → Stack : ₄ then pop 4.

If we print every node after pop it will somehow look like,

PATH - 5 8 9 7 6 3 4




Similarly, we can do it for a graph by starting with the insertion of any node and popping every node while the stack is not empty and pushing every adjacent elements of a popped node.

Now it's time to understand the concept via c++ code so without wasting any time let's directly dive into it :




💡 You are given input in a format such as first line contains two spaceseparated integers 'N' & 'M' which tells the number of nodes and number of edges respectively. Then 'M' lines contain two spaceseparated integers 'u' & 'v' 1≤{u, v} N determines the edge between those two nodes.






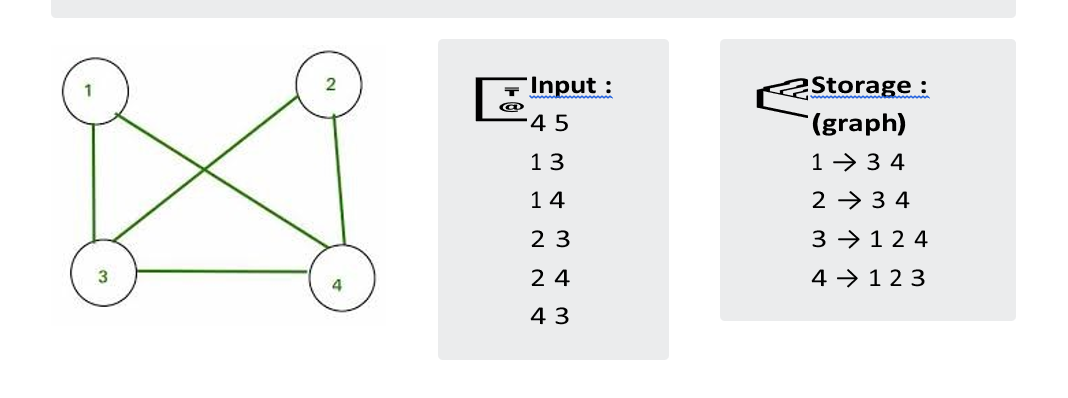
Time Complexity : the time complexity is O ( V + E ) where V is the number of vertexes and E is the number of edges.




DFS using Recursion :




Also as we know whatever we can do with using stack same thing we can achieve using recursion also. Therefore, in this case, also we can code DFS using recursion which is quite preferable and shorter than using stack.




💡 You are given input in a format such as the first line contains an integer 'N' which tells the number of nodes. Then 'N1' lines contain two space-separated integers 'u' & 'v' 1≤{u, v} N determines the edge between those two nodes.






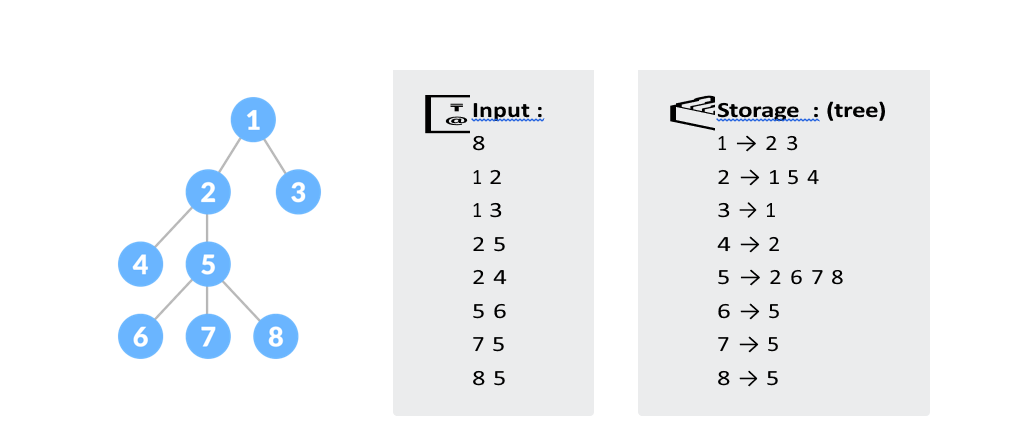
Here, below given two implementations of DFS using recursion both will show the same output. It just depends upon the need according to the problem we can use either of them.

tree → 2D dynamic array, globally declared and elements of this is the one represented in a storage section.